Author: David Chasteen-Boyd
Introduction to prime numbers
Think back to elementary school during which you learned about a seemingly useless mathematical relic called prime numbers. Your teacher told you in class one day that they are special numbers, divisible only by themselves and one. You also learned about prime factorization, or factor trees, in which you kept dividing a number until it could be divided no further. Then you were given a worksheet, which you scrambled to finish so you could go to recess, and promptly forgot about prime numbers until it was time to take that standardized test at the end of the school year.
As it turns out, prime numbers are incredibly important in math and even in fields as far-reaching as quantum physics and Internet security. They are often referred to as the building blocks of all numbers. Composite numbers, integers that are not prime, are made up of prime numbers combined together in some way. One way of forming composite numbers is by reversing the process of prime factorization: instead of dividing a composite number into its prime number components, you can multiply prime numbers together to form a composite number. Prime numbers have been studied for thousands of years. The Greek mathematician Euclid showed that every number is either prime or the product of prime numbers and proved that there are infinitely many prime numbers. Other theories of prime numbers include the twin primes conjecture, which states that there are infinitely many "pairs" of prime numbers that are only two units away from each other (the larger prime minus the smaller prime equals 2, such as with 41 and 43). However, despite thousands of years of study and great interest, there are still many unanswered questions in analytic number theory, which is the study of the properties of integers and prime numbers. One of the most significant of these questions is the Riemann hypothesis.
At its core, the Riemann hypothesis seeks to find and study the pattern and distribution of prime numbers as they get larger and larger. Consider the pattern in the first four prime numbers: 2, 3, 5, and 7. At first glance, it seems like all of the odd numbers less than 10 are prime, but then comes 9. Still, it seems like most odd numbers are prime. The next few are 11, 13, 17, 19, and 23. That set initially increases by increments of 2 or 4 but then suddenly jumps up by 6. The next set of primes is 29, 31, 37, 41, 43, and 47. The spacing between them seems to be increasing, until you reach the primes 71 and 73. So, what exactly is the pattern? Are the primes getting farther apart or closer together with increasing magnitude? Or is the average distance between them staying the same?
The Prime Number Theorem, which Riemann first tried to prove when he was proposing his hypothesis, states that the average distance between the primes in the first N integers after 0 can be approximated using the following formula
D = ln(N)
where ln is the natural logarithm (the inverse of ex). However, it is important to remember that this average distance is an approximate value: the natural log function only approximates the location of primes over a large interval, not in small regions. The natural log function is analogous to a forest; even though you may know where the forest is, it is still hard to find the specific tree that you are looking for. Furthermore, the actual distance between two consecutive prime numbers is difficult or impossible to predict. Since the Prime Number Theorem was proven, many increasingly accurate approximations for the distribution of prime numbers have been discovered1. However, no function yet exists that reveals exactlywhere each prime is located on the number line.
What is the Riemann hypothesis?
The Riemann hypothesis itself states that the zeros of a particular function, known as the Riemann zeta function, all lie along a specific line in what is known as the complexplane. The zeros of this function act the same as the roots of a quadratic equation –plugging them into the function as its values causes the function to equal zero. However, determining these values is difficult due to the fact that the Riemann zeta function is a complex-valued function. In this case, complex means that it contains complex numbers, numbers which have both a real and imaginary component and have the form a + bi where i is the square root of negative one. Because of this property, the function’s domain is plotted on the complex plane, in which the horizontal axis represents real numbers and the vertical axis represents imaginary numbers. Because the zeta function is a complex-valued function, its roots must also be plotted in the complex plane.
There are two types of roots of the Riemann zeta function. The first type is called the trivial zeros, which are all of the negative even integers. The second type, the nontrivial zeros, which are more complicated than the trivial zeros, is the type that the Riemann hypothesis seeks to define. Riemann showed in his 1859 paper2 that all of the nontrivial solutions to the Riemann zeta function lie in a region of the complex plane known as the critical strip – the region between 0 and 1 on the real axis that extends infinitely upwards in the imaginary direction (Figure 1). Riemann proposed that all of the nontrivial zeros of the function might lie on an even more specific region of the complex plane: the vertical line whose values all have a real part equal to ½; this statement is the Riemann hypothesis. Interestingly, this vertical line is located in the center of the critical strip.
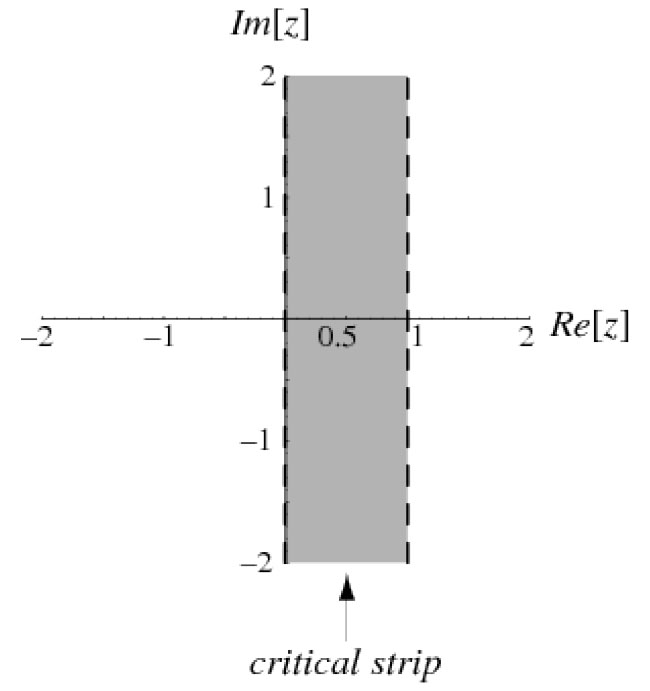
Image Caption: Figure 1 | The complex plane, showing the critical strip3.
The form of the zeros to the Riemann zeta function implies much about the distribution of the prime numbers along the number line. So if the Riemann hypothesis is proven correct in that all of the solutions to the Riemann zeta function do have the form ½ + bi, we will gain insight into the locations of the prime numbers and how much they deviate from the functions that the Prime Number Theorem presents.
Why should non-mathematicians care?
Though few people other than mathematicians may find it interesting to discuss the location and distribution of the primes, the Riemann hypothesis is relevant to other fields as well. Recent research has suggested that the locations of the zeros of the zeta function might have implications in quantum physics. A relatively recent field of research in quantum physics, quantum chaos, studies quantum systems that behave like classical chaotic systems (like a double pendulum or a billiard ball on a nonrectangular table). The defining equations of quantum chaotic systems belong to a class of equations known as trace equations.
As it turns out, the Riemann zeta function can also be written as a trace equation. It is therefore possible to create a quantum chaotic system whose behavior is defined by the Riemann zeta function. Mathematicians and physicists are hopeful that studying this system could lead to a better understanding of the zeta function, and vice versa. However, this application pales in comparison to the effect that the Riemann hypothesis could have on a field of globalimportance: Internet security and encryption.
Creating a factor tree involves a lot of tedious labor: going one by one through the number line to find a factor of the number, and repeating this process for each factor until only prime numbers are left. Imagine trying to factor a number that is near 10600, instead of one that is only in the tens or hundreds. For comparison, the total number of atoms in the universe is approximately 1080 [4]. This number would take a lifetime, if not longer, to factor, and computers are not much more efficient than humans at large number factorization. Modern encryption methods take advantage of this weakness.
The basic mechanism through which modern encryption methods work hinges on the fact that computers take a long time to factor large numbers. One type of encryption, developed by RSA Security, LLC, uses public key encryption5. There are two main components to this type of encryption: the encryption key, which is made public, and the decryption key, which is kept secret. The decryption key is composed of two large prime numbers that are near 10300 digits long. The encryption key is the product of those two numbers, which is near 10600 digits long. The encryption key allows those who would like to send messages to encrypt them so that they cannot be read or manipulated by outside parties. The only parties that can decrypt the coded message and read it properly are those that have access to the decryption key. Because of the time required to factor such a large number, and because of other mathematical manipulations performed on the keys in order to obfuscate the original numbers, it is almost impossible to obtain the decryption key unless it is given to you.
The ethics of Riemann hypothesis research
Because of the implicationsthat the Riemann hypothesis could have on our understanding of the distribution of prime numbers, especially large prime numbers, it is possible that a proof for the Riemann hypothesis could lead to quicker and easier methods of finding large primes. Thiscould in turn lead to the breakdown of modern encryption methods because choosing numbers to use as potential factors of the encryption key would be more efficient. Basically, if we already know where the primes are, we only have to pick those as factors instead of picking every number. Many processes that are carried out online and intended to be secure, such as banking transactions and military and government communications, could potentially no longer be sufficiently protected. Despite this security threat, a solution to the Riemann hypothesis could also provide beneficial applications. Its potential to improve our understanding of quantum physics could lead to improved and innovative technologies. Furthermore, recent research has shown that the zeta function has a strong connection to quantum mechanics, and many mathematicians are optimistic that a novel approach combining physics and math could be the motivation that researchers in this field need to finally find a solution.
The potential negative consequences of finding a solution to the Riemann hypothesis create an ethical dilemma for researchers to consider. Mathematicians and scientists dedicate their lives to the pursuit of knowledge, often just for knowledge’s sake. However, is it morally right to pursue something that could have such a devastating global impact? Is there a certain point at which the potential benefits of new knowledge are outweighed by the damage it could cause? It seems that a proof for the Riemann hypothesis is still, at the veryleast, a few years away; therefore, a global internet security issue should not exist anytime in the near future. Perhaps this potential for harm also presents a new impetus for computer scientists to develop new, more secure encryption algorithms that donot depend on prime numbers, thereby encouraging further innovation and progress.
References
- Cipra, B. A prime case of chaos. What's Happening in the Mathematical Sciences 4, Ams.org. Retrieved from http://www.ams.org/samplings/math-history/prime-chaos.pdf (1999).
- Riemann, B. On the Number of Primes Less Than a Given Magnitude. Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin (1859).
- Weisstein, E.W.Critical Strip. From MathWorld—A Wolfram Web Resource. Retrieved from http://mathworld.wolfram.com/CriticalStrip.html.
- Devlin, K.J. The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of Our Time. New York: Basic (2002).
- Rivest, R.L.,Shamir, A. & Adleman, L.A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21 (2), 120-126(1978).
